ปริมาณทางฟิสิกส์

1. ความหมายของวิทยาศาสตร์

วิทยาศาสตร์ (Science) หมายถึง การศึกษาหาความจริงเกี่ยวกับปรากฏการณ์ทางธรรมชาติรอบๆ ตัวเรา ทั้งที่มีชีวิตและไม่มีชีวิต อย่างมีขั้นตอนและระเบียบแบบแผน วิทยาศาสตร์แบ่งออกได้ดังนี้

1. วิทยาศาสตร์บริสุทธิ์ (Pure Science) หรือ วิทยาศาสตร์ธรรมชาติ (Natural Science) เป็นการศึกษาหาความจริงใหม่ๆ เกี่ยวกับปรากฏการณ์ทางธรรมชาติ เพื่อนำไปสู่กฎเกณฑ์และทฤษฎีต่างๆ ทางวิทยาศาสตร์ เช่น กฎการเคลื่อนที่ของนิวตัน กฎของโอห์ม ทฤษฎีสัมพัทธภาพของไอน์สไตน์ ทฤษฎีคลื่นแม่เหล็กไฟฟ้าของแมกซ์เวลล์ เป็นต้น วิทยาศาสตร์บริสุทธิ์แบ่งออกเป็น 2สาขาคือ ก. วิทยาศาสตร์กายภาพ (Physical Science) ศึกษาค้นคว้าเกี่ยวกับสิ่งไม่มีชีวิต เช่น ฟิสิกส์ เคมี ดาราศาสตร์ ธรณีวิทยา เป็นต้น ข. วิทยาศาสตร์ชีวภาพ (Biological Science) ศึกษาค้นคว้าเกี่ยวกับสิ่งมีชีวิต เช่น พฤกษศาสตร์ สัตวศาสตร์ เป็นต้น 2. วิทยาศาสตร์ประยุกต์ (Applied Science) เป็นการนำความรู้จากกฎเกณฑ์หรือทฤษฎีของวิทยาศาสตร์บริสุทธิ์ มาประยุกต์เป็นหลักการทางเทคโนโลยี เพื่อนำไปใช้ให้เกิดประโยชน์แก่สังคม เช่น วิศวกรรมศาสตร์ แพทยศาสตร์ สถาปัตยกรรมศาสตร์ เป็นต้น2. การค้นคว้าหาความรู้ทางวิทยาศาสตร์ การค้นคว้าหาความรู้ทางวิทยาศาสตร์ ความรู้ทางวิทยาศาสตร์เป็นการค้นคว้าหาความจริงจากปรากฏการณ์ทางธรรมชาติ ซึ่งสามารถทำได้ 3 แนวทางคือ1. จากการสังเกตปรากฏการณ์ทางธรรมชาติ2. จากการทดลองในห้องปฏิบัติการ

จากการสร้างแบบจำลอง (Model) ทางความคิด

3. ฟิสิกส์

เป็นวิทยาศาสตร์แขนงหนึ่ง ศึกษาธรรมชาติของสิ่งไม่มีชีวิต ซึ่งได้แก่ การเปลี่ยนแปลงทางกายภาพและปรากฏการณ์ต่างๆ ที่เกิดขึ้นรอบตัวเรา การค้นคว้าหาความรู้ทางฟิสิกส์ทำได้โดยการสังเกต การทดลอง และการเก็บข้อมูลมาวิเคราะห์เพื่อสรุปผลเป็นทฤษฎี หลักหรือกฎ ความรู้เหล่านี้ สามารถนำไปใช้อธิบายปรากฏการณ์ธรรมชาติ หรือทำนายสิ่งที่อาจเกิดขึ้นในอนาคตและความรู้นี้สามารถนำไปใช้เป็นพื้นฐานในการแสวงหาความรู้ใหม่เพิ่มเติม และพัฒนาคุณภาพชีวิตของมนุษย์

ความสำคัญของการศึกษาทางด้านฟิสิกส์ คือข้อมูลที่มีผลต่อการเปลี่ยนแปลงกฎและทฤษฎีที่มีอยู่เดิม ข้อมูลที่ได้นี้แบ่งออกเป็น 2ประเภท คือ

ข้อมูลเชิงคุณภาพ (Qualitative Data) เป็นข้อมูลที่ไม่เป็นตัวเลข ได้จากการสังเกตตามขอบเขตของการรับรู้ เช่น รูปร่าง ลักษณะ กลิ่น สี รส เป็นต้น

ข้อมูลเชิงปริมาณ (Quantitative Data) เป็นข้อมูลที่เป็นตัวเลข ได้จากการวัดปริมาณต่างๆโดยใช้เครื่องมือวัดและวิธีการวัดที่ถูกต้อง เช่น มวล ความยาว เวลา อุณหภูมิ เป็นต้น

4. เทคโนโลยี

เป็นวิทยาการที่เกี่ยวข้องกับศิลปะ ในการสร้าง การผลิต หรือการใช้อุปกรณ์ เพื่อก่อให้เกิดประโยชน์กับมนุษย์โดยตรง

5. ปริมาณกายภาพ ปริมาณกายภาพ ( Physical Quantity ) เป็นปริมาณทางฟิสิกส์ที่ได้จากข้อมูลเชิงปริมาณ เช่น มวล แรง ความยาว เวลา อุณหภูมิ เป็นต้น ปริมาณกายภาพแบ่งออกเป็น 2 ชนิด คือ

1. ปริมาณฐาน ( Base Unit ) เป็นปริมาณหลักของระบบหน่วยระหว่างชาติ มี 7 ปริมาณ ดังนี้

ปริมาณฐาน	ชื่อหน่วย	สัญลักษณ์
ความยาว	เมตร	m
มวล	กิโลกรัม	kg
เวลา	วินาที	s
กระแสไฟฟ้า	แอมแปร์	A
อุณหภูมิ,อุณหพลวัต	เคลวิน	K
ปริมาณสาร	โมล	mol
ความเข้มของการส่องสว่าง	แคนเดลา	cd

2. ปริมาณอนุพัทธ์ (Derived Unit) เป็นปริมาณที่ได้จากปริมาณฐานตั้งแต่ 2 ปริมาณขึ้นไปมาสัมพันธ์กัน ดังตัวอย่างต่อไปนี้

ปริมาณอนุพัทธ์	ชื่อหน่วย	สัญลักษณ์	เทียบเป็นหน่วยฐานและอนุพัทธ์อื่น
ความเร็ว	เมตรต่อวินาที	m/s,	1 m / s =
ความเร่ง	เมตรต่อวินาที²	m /s²	1 m / s² =
แรง	นิวตัน	N	1 N = 1 kg. m /s²
งาน,พลังงาน	จูล	J	1 J = 1 N.m
กำลัง	วัตต์	W	1 W = 1 J /s
ความดัน	พาสคาล	Pa	1 Pa = 1 N / m²
ความถี่	เฮิรตซ์	Hz	1 Hz = 1 s^{– 1}

6. ระบบหน่วยระหว่างชาติ ในสมัยก่อนหน่วยที่ใช้สำหรับวัดปริมาณต่างๆ มีหลายระบบ เช่น ระบบอังกฤษ ระบบเมตริกและระบบของไทย ทำให้ไม่เป็นมาตรฐานเดียวกัน ดังนั้นปัจจุบันหลายๆประเทศ รวมทั้งประเทศไทยด้วยได้ใช้หน่วยสากลที่เรียกว่า ระบบหน่วยระหว่างชาติ (The International System of Unit) เรียกย่อว่า ระบบเอสไอ (SI Units) ซึ่งประกอบด้วยหน่วยฐาน และหน่วยอนุพัทธ์ ดังนี้

1. หน่วยฐาน (Base Unit ) เป็นปริมาณหลักของระบบหน่วยระหว่างชาติ มี 7 ปริมาณ ดังนี้

ปริมาณฐาน	ชื่อหน่วย	สัญลักษณ์
ความยาว	เมตร	m
มวล	กิโลกรัม	kg
เวลา	วินาที	s
กระแสไฟฟ้า	แอมแปร์	A
อุณหภูมิ,อุณหพลวัต	เคลวิน	K
ปริมาณสาร	โมล	mol
ความเข้มของการส่องสว่าง	แคนเดลา	cd

2. หน่วยอนุพัทธ์ (Derived Unit) เป็นปริมาณที่ได้จากปริมาณฐานตั้งแต่ 2 ปริมาณขึ้นไปมาสัมพันธ์กัน ดังตัวอย่างต่อไปนี้

ปริมาณอนุพัทธ์	ชื่อหน่วย	สัญลักษณ์	เทียบเป็นหน่วยฐานและอนุพัทธ์อื่น
ความเร็ว	เมตรต่อวินาที	m/s	1 m / s =
ความเร่ง	เมตรต่อวินาที²	m /s²	1 m / s² =
แรง	นิวตัน	N	1 N = 1 kg. m /s²
งาน พลังงาน	จูล	J	1 J = 1 N.m
กำลัง	วัตต์	W	1 W = 1 J /s
ความดัน	พาสคาล	Pa	1 Pa = 1 N / m²
ความถี่	เฮิรตซ์	Hz	1 Hz = 1 s^{– 1}

7. การบันทึกปริมาณที่มีค่ามากหรือน้อย ผลที่ได้จากการวัดปริมาณทางวิทยาศาสตร์ บางครั้งมีค่ามากกว่าหรือน้อยกว่า 1มากๆ ทำให้เกิดความยุ่งยากในการนำไปใช้งาน ดังนั้น การบันทึกปริมาณดังกล่าว เพื่อให้เกิดความสะดวกในการนำไปใช้สามารถทำได้ 2 วิธี คือ

0.000 x10 ^±ⁿ

จำนวนเต็ม 1 ตำแหน่ง

เท่ากับจำนวนตัวเลขหลังจุดหรือตัวเลขระหว่างจุด

7.1 เขียนให้อยู่ในรูปของจำนวนเต็มหนึ่งตำแหน่ง ตามด้วยเลขทศนิยม แล้วคูณด้วยเลขสิบยกกำลังบวกหรือลบดังนี้ตัวอย่าง จงเขียนปริมาณต่อไปนี้ในรูปเลขยกกำลัง ก. 360,000,000 เมตร ข. 6,539,000 กิโลเมตร

ค. 0.00048 กิโลกรัม ง. 0.00127 วินาที

วิธีทำ ก. 360,000,000 เมตร = 360,000,000 = 3.6x10⁸ เมตร ข. 6,539,000 กิโลเมตร = 6,539,000 = 6.5x10⁶ กิโลเมตร = 6.5 x 10⁹ เมตร ค. 0.00048 กิโลกรัม = 0.00048 = 4.8x10^{– 4} กิโลกรัม ง. 0.00127 วินาที = 0.00127 = 1.27x10^{- 5} วินาที 7.2 เขียนโดยใช้คำ “อุปสรรค” ( Prefix)

คำอุปสรรค คือ คำที่ใช้เติมหน้าหน่วย SI เพื่อทำให้หน่วย SI ใหญ่ขึ้นหรือเล็กลง ดังแสดงในตาราง

คำอุปสรรค	สัญลักษณ์	ตัวพหุคูณ	คำอุปสรรค	สัญลักษณ์	ตัวพหุคูณ
เทอรา	T	10¹²	พิโค	P	10^-12
จิกะ	G	10 ⁹	นาโน	n	10 ^{- 9}
เมกะ	M	10⁶	ไมโคร	m	10^{– 6}
กิโล	k	10³	มิลลิ	m	10^{– 3}
เฮกโต	h	10²	เซนติ	c	10^{– 2}
เดคา	da	10	เดซิ	d	10^{- 1}

ตัวอย่าง จงเขียนปริมาณต่อไปนี้ โดยใช้คำอุปสรรค ก. ความยาว 12 กิโลเมตร ให้มีหน่วยเป็น เมตร ข. มวล 0.00035 เมกะกรัม ให้มีหน่วยเป็น มิลลิกรัมวิธีทำ

ก. เปลี่ยน กิโล ® เมตร	ข. เปลี่ยน เมกะ ® กิโล ® กรัม ® มิลลิ
= 12 x 10³	= 0.00035 x 10³ x 10³ x 10³
= 1.2 x 10⁴ เมตร	= 0.00035 x 10⁹
	= ( 3.5 x 10^{– 4} ) x 10⁹
	= 3.5 x 10⁵ มิลลิกรัม

่

ปริมาณเวกเตอร์

ปริมาณกายภาพแบ่งออกได้ 2 ประเภท

1. ปริมาณสเกล่าร์ คือปริมาณที่บอกแต่ขนาดอย่างเดียวก็ได้ความหมายสมบูรณ์ ไม่ต้องบอกทิศทาง เช่น ระยะทาง มวล เวลา ปริมาตร ความหนาแน่น งาน พลังงาน ฯลฯ
การหาผลลัพธ์ของปริมาณสเกล่าร์ ก็อาศัยหลังการทางพีชคณิต คือ วิธีการ บวก ลบ คูณ หาร
2. ปริมาณเวกเตอร์ คือ ปริมาณที่ต้องบอกทั้งขนาดและทิศทาง จึงจะได้ความหมายสมบูรณ์ เช่น การกระจัด ความเร่ง ความเร็ว แรง โมเมนตัม ฯลฯ
การหาผลลัพธ์ของปริมาณเวกเตอร์ ต้องอาศัยวิธีการทางเวคเตอร์ โดยต้องหาผลลัพธ์ทั้งขนาดและทิศทาง

ปริมาณเวกเตอร์

1. สัญลักษณ์ของปริมาณเวกเตอร์

ใช้อักษรมีลูกศรครึ่งบนชี้จากซ้ายไปขวา หรือใช้ตัวอักษรทึบแสดงปริมาณเวกเตอร์ก็ได้

2. เวกเตอร์ที่เท่ากัน

เวกเตอร์ 2 เวกเตอร์เท่ากัน เมื่อเวกเตอร์ทั้งสองเท่ากันและมีทิศไปทางเดียวกัน

3. เวกเตอร์ลัพธ์ใช้อักษร R

4. การบวก-ลบเวกเตอร์

การบวก-ลบเวกเตอร์ หรือการหาเวกเตอร์ สามารถทำได้ 2 วิธี คือ

1. วิธีการเขียนรูป

2. วิธีการคำนวณ

1.1 การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีขั้นตอนดังนี้

(1) เขียนลูกศรตามเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด

(2) นำหางลูกศรของเวกเตอร์ที่ 2 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์แรก

(3) นำหางลูกศรของเวกเตอร์ที่ 3 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์ที่ 2

(4) ถ้ามีเวกเตอร์ย่อยๆอีก ให้นำเวกเตอร์ต่อๆไป มากระทำดังข้อ (3) จนครบทุกเวกเตอร์

(5) เวกเตอร์ลัพธ์หาได้โดยการลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวของเวกเตอร์สุดท้าย เช่น

นิยามต้องทราบ
ถ้า A เป็นเวกเตอร์ใดๆที่มีขนาดและทิศทางหนึ่งๆ เวกเตอร์ -A คือ เวกเตอร์ที่มีขนาดเท่ากับเวกเตอร์ A แต่ มี ทิศทางตรงกันข้าม

1.2 การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
เนื่องจากการหาเวกเตอร์ลัพธ์โดยวิธีการวาดรูป ให้ผลลัพธ์ไม่แม่นยำเพียงแต่ได้คร่าวๆ เท่านั้น เพราะถ้าลากความยาวหรือทิศทางลูกศรแทนเวกเตอร์คลาดเคลื่อนเพียงเล็กน้อย ผลของเวกเตอร์ลัพธ์ก็จะคลาดเคลื่อนไปด้วยแต่การหาเวกเตอร์ลัพธ์โดยการคำนวณจะให้ผลลัพธ์ถูกต้องแน่นอน

การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ เมื่อมีเวกเตอร์ย่อยเพียง 2 เวกเตอร์ จะแบ่งออกเป็น 3 ลักษณะ ดังนี้
1. เวกเตอร์ทั้ง 2 ไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของขนาดเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ไปทางเดียวกับเวกเตอร์ทั้งสอง
2. เวกเตอร์ทั้ง 2 สวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
เพราะฉะนั้น R = B - A เมื่อ B > A , R = A - B เมื่อ A > B
3. เวกเตอร์ทั้ง 2 ทำมุม 0 ต่อกัน สามารถหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปสี่เหลี่ยมด้านขนาน โดยให้เวกเตอร์ย่อยเป็นด้านของสี่เหลี่ยมด้านขนานที่ประกอบ ณ จุดนั้น จะ ได้เวกเตอร์ลัพธ์มีขนาดและทิศทางตามแนวเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่ลากจากจุดที่เวกเตอร์ทั้งสองกระทำต่อกัน

ระยะทาง (Distance) คือ ความยาววัดตามแนวเส้นที่อนุภาคเคลื่อนที่ เป็นปริมาณสเกล่าร์(มีเฉพาะขนาด)หน่วยมาตรฐาน SI คือ "เมตร"
การขจัด หรือ การกระจัด (Displacement) คือ เส้นตรงที่ลากจากจุดตั้งต้นของการเคลื่อนที่ไปยังจุดสุดท้ายของการเคลื่อนที่ เป็นปริมาณเวกเตอร์ มีทั้งขนาดและทิศทาง (คือ ทิศจากที่หัวศรลากจากจุดตั้งต้นไปสุดท้าย)มีหน่วย "เมตร" เช่นกัน

ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่
ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่จะเป็นพื้นฐานในการศึกษาเรื่องของการเคลื่อนที่ ซึ่งในการเคลื่อนที่จะต้องประกอบไปด้วยองค์ประกอบ 3 ส่วนY วัตถุที่เคลื่อนที่ จะหมายจึงวัตถุที่มีลักษณะเป็นของแข็งที่คงรูปทรงอยู่ได้
Y ผู้สังเกต เป็นผู้ที่ศึกษาวัตถุที่เคลื่อนที่ โดยผู้สังเกตจะต้องอยู่นอกวัตถุที่เคลื่อนที่
Y จุดอ้างอิง การเคลื่อนที่ของวัตถุจะต้องมีการเปลี่ยนตำแหน่งของวัตถุดังนั้นเราจะต้องมีจุดอ้างอิง
เพื่อบอกตำแหน่งของวัตถุเมื่อเวลาผ่านไป

1. ระยะทาง (Distance) การเคลื่อนที่ของวัตถุจะเริ่มนับตั้งแต่จุดเริ่มต้นที่เราสังเกตเป็นจุดอ้างอิงแล้ววัดระยะทางตามแนวทางที่วัตถุเคลื่อนที่
ไปตามแนวทางการเคลื่อนที่ของวัตถุ

2. การกระจัด (Displacement) เป็นการบอกตำแหน่งของวัตถุหลังจากการที่เคลื่อนที่ไปแล้วในช่วงเวลาหนึ่งโดยจะบอกว่าห่างจากจุดเริ่มต้นเป็นระยะ
เท่าไร และอยู่ทางทิศไหนของจุดเริ่มต้น ดังนั้นการกระจัดเป็น ปริมาณเวกเตอร์ เพราะมีทั้งขนาดและทิศทาง
*********ถ้าวัตถุเคลื่อนที่กลับมาสู่จุดเริ่มต้น การกระจัดจะมีค่าเป็นศูนย์**********

3. เวลา (Time) การวัดเวลาเรานับ ณ จุดเริ่มสังเกต ซึ่งขณะนั้นวัตถุอาจจะหยุดนิ่ง หรือเคลื่อนที่อยู่ก็ตาม ค่าของเวลาจะมีความสัมพันธ์กับระยะทาง เมื่อเวลาผ่านไป ระยะทางที่วัตถุเคลื่อนที่ก็จะเพิ่มขึ้น ในบางครั้งอาจจะมีข้อมูลของระยะทางกับเวลาสัมพันธ์กัน

4. อัตราเร็ว (Speed) หมายถึง ระยะทางที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา เป็นปริมาณสเกลาร์ มีหน่วยเป็น เมตร/วินาที

V แทน อัตราเร็ว มีหน่วยเป็น เมตร/วินาที (m/s)

S แทน ระยะทาง มีหน่วยเป็น เมตร (m)

t แทน เวลา มีหน่วยเป็น วินาที (s )

5. ความเร็ว (Velocity) หมายถึง การกระจัดของวัตถุที่เปลี่ยนไปในหน่วยเวลา

แทน ความเร็ว มีหน่วยเป็น เมตร/วินาที (m/s)

แทน การกระจัด มีหน่วยเป็น เมตร (m)

t แทน เวลา มีหน่วยเป็น วินาที (s )

6. ความเร่ง (Acceleration) ความเร็วที่เปลี่ยนไปในหนึ่งหน่วยเวลา

แทน ความเร่ง มีหน่วยเป็น เมตร/วินาที2 (m/s2 )

แทนความเร็วที่เปลี่ยนไป มีหน่วยเป็น เมตร/ วินาที(m/s)

แทน เวลา มีหน่วยเป็น วินาที (s )

ลักษณะของการเคลื่อนที่ลักษณะของการเคลื่อนที่แบ่งได้ 4 ลักษณะ คือ
1. การเคลื่อนที่เป็นแนวเส้นตรง
ลักษณะของการเคลื่อนที่แบบนี้เป็นพื้นฐานของการเคลื่อนที่ เพราะทิศทางการเคลื่อนที่จะมีทิศทางเดียว
แต่อาจจะเคลื่อนที่ไป-กลับได้ รูปแบบการเคลื่อนที่อาจจะแตกต่างกันออกไป ตัวอย่างเช่น
- การเคลื่อนที่ของรถไฟบนราง
- การเคลื่อนที่ของรถบนถนนที่เป็นแนวเส้นตรง
- การเคลื่อนที่ภายใต้แรงโน้มถ่วงของโลก
2. การเคลื่อนที่แบบโพรเจกไทล์
เป็นการเคลื่อนที่ของวัตถุที่มีแนวเส้นทางการเคลื่อนที่เป็นรูปโค้งพาราโบลา และเป็นพาราโบลาทางแกน y
ที่มีลักษณะคว่ำการที่วัตถุเคลื่อนที่เป็นแนวเส้นโค้งเนื่องจากวัตถุเคลื่อนที่เข้าไปในบริเวณที่มีแรงกระทำต่อ
วัตถุไม่อยู่ในแนวเดียวกับทิศของการเคลื่อนที่

3. การเคลื่อนที่แบบวงกลม
เป็นการเคลื่อนที่ของวัตถุรอบจุดๆหนึ่ง โดยมีรัศมีคงที่ การเคลื่อนที่เป็นวงกลม
ทิศทางของการเคลื่อนที่จะเปลี่ยนแปลงตลอดเวลา ความเร็วของวัตถุจะเปลี่ยนไปตลอดเวลา ทิศของแรงที่กระทำจะตั้งฉากกับทิศของการเคลื่อนที่
แรงที่กระทำต่อวัตถุจะมีทิศทางเข้าสู่ศูนย์กลาง เราจึงเรียกว่า “แรงสู่ศูนย์กลาง”
ในขณะเดียวกัน จะมีแรงต้านที่ไม่ให้วัตถุเข้าสู่ศูนย์กลาง เราเรียกว่า “แรงหนีศูนย์กลาง” แรงหนีศูนย์กลางจะเท่ากับแรงสู่ศูนย์กลาง วัตถุจึงจะเคลื่อนที่เป็นวงกลมได้

4. การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
ลักษณะของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย จะเป็นการเคลื่อนที่ที่มีลักษณะ
พิเศษ คือ วัตถุจะเคลื่อนที่กลับไปกลับมาที่เราเรียกว่า แกว่ง หรือ สั่น การเคลื่อนที่แบบนี้จะเป็นการเคลื่อนที่อยู่ในช่วงสั้นๆ มีขอบเขตจำกัด เราเรียกว่า แอมพลิจูด (Amplitude) โดยนับจากตำแหน่งสมดุล ซึ่งอยู่ตรงจุดกลางวัดไปทางซ้ายหรือขวา เช่น การแกว่งของชิงช้า หรือยานไวกิงในสวนสนุก

รูป การสั่นและแกว่งของวัตถุ

ระยะทาง

บุคคลยืนอยู่ในระยะทางต่างๆ กัน

ระยะทาง หมายถึงตัวเลขที่อธิบายว่า วัตถุแต่ละอย่างอยู่ห่างกันเท่าไรในช่วงเวลาหนึ่ง ในทางฟิสิกส์ ระยะทางอาจหมายถึงความยาวทางกายภาพ ระยะเวลา หรือการประมาณค่าบนสิ่งที่พิจารณาสองอย่าง ส่วนทางคณิตศาสตร์จะพิจารณาอย่างเฉพาะเจาะจงมากกว่า โดยทั่วไปแล้ว "ระยะทางจาก A ไป B" มีความหมายเหมือนกับ "ระยะทางระหว่าง A กับ B"

[แก้]เรขาคณิตคณิตศาสตร์

[แก้]

ในเรขาคณิตสัมบูรณ์ (absolute geometry) ระยะทางที่น้อยที่สุดระหว่างจุดสองจุด คือความยาวของส่วนของเส้นตรงที่เชื่อมระหว่างจุดเหล่านั้น

ในเรขาคณิตเชิงพีชคณิต (algebraic geometry) เราสามารถหาระยะทางระหว่างจุดสองจุดบนระนาบ xy โดยใช้สูตรต่อไปนี้ ระยะทางจาก (x₁, y₁) ไปยัง (x₂, y₂) คำนวณได้จาก

$d=\sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\,$

และในกรณีเดียวกัน ระยะทางจาก (x₁, y₁, z₁) ไปยัง (x₂, y₂, z₂) บนปริภูมิสามมิติ คำนวณได้จาก

$d=\sqrt{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

ซึ่งสามารถพิสูจน์ได้ง่ายโดยการสร้างรูปสามเหลี่ยมมุมฉาก แล้วคำนวณหาความยาวของด้านตรงข้ามมุมฉาก (hypotenuse) โดยใช้ทฤษฎีบทพีทาโกรัส

ในการศึกษาเรขาคณิตในระดับที่ซับซ้อน เราจะเรียกการหาระยะทางแบบนี้ว่าเป็น ระยะทางแบบยุคลิด (Euclidean distance) ซึ่งขยายผลมาจากทฤษฎีบทพีทาโกรัส แต่จะไม่ครอบคลุมถึงเรขาคณิตนอกแบบยุคลิด (non-Euclidean geometry) สูตรการหาระยะทางข้างต้นสามารถนำไปประยุกต์ใช้กับความยาวส่วนโค้ง (arc length) ได้ด้วย

[แก้]กรณีทั่วไป

ฟังก์ชันระยะทาง d บนเซต M ที่เป็นเซตของจุด กำหนดขึ้นโดยที่ d : M×M → ℝ จะทำให้เงื่อนไขต่อไปนี้เป็นจริง

d(x, y) ≥ 0 และ d(x, y) = 0 ก็ต่อเมื่อ x = y (ระยะทางระหว่างจุดสองจะเป็นจำนวนบวก และจะเป็นศูนย์ก็ต่อเมื่ออยู่ที่จุดเดียวกัน)
d(x, y) = d(y, x) (ระยะทางระหว่างจุดสองจุดจะเท่ากันโดยไม่คิดทิศทาง)
d(x, z) ≤ d(x, y) + d(y, z) (ระยะทางระหว่างจุดสองจุด จะสั้นกว่าหรือเท่ากับระยะทางรวมที่ผ่านจุดอื่น)

ซึ่งฟังก์ชันระยะทางจะก่อให้เกิดปริภูมิอิงระยะทาง (metric space) ที่ประกอบด้วยคู่อันดับ (M, d)

[แก้]ระยะทางกับระยะกระจัดระยะทางที่นับโดยยานพาหนะ (ด้วย มาตรระยะทาง) หรือโดยคน สัตว์ สิ่งของ ฯลฯ ควรแยกแยะออกจากระยะกระจัดระหว่างจุดเริ่มต้นถึงจุดสิ้นสุด ถึงแม้ว่าจะหมายถึงระยะทางที่สั้นที่สุดก็ตาม เนื่องจากเส้นทางอาจมีการวนรอบ ซึ่งจุดสิ้นสุดสามารถเป็นจุดเดียวกับจุดเริ่มต้นก็ได้

ระยะทางเป็นปริมาณสเกลาร์ที่ไม่สามารถเป็นจำนวนลบ และมีเพียงขนาด (magnitude) ในขณะที่ระยะกระจัด (displacement) จะเทียบเท่ากับปริมาณเวกเตอร์ที่มีทั้งขนาดและทิศทาง

การกระจัด

การกระจัด หรือ การขจัด ในทางฟิสิกส์ หมายถึงระยะห่างของการเคลื่อนที่จากจุดเริ่มต้นไปยังจุดสุดท้ายโดยจะมีลักษณะเป็นเส้นตรง ซึ่งจะเป็นระยะทางที่สั้นที่สุดระหว่างจุดสองจุดใด ๆ ในขณะที่เราเคลื่อนที่ เราจะเปลี่ยนตำแหน่งที่อยู่ตลอดแนว เช่น ขณะเราขับรถยนต์ไปตามท้องถนน เราจะเคลื่อนที่ผ่านถนน ถนนอาจเป็นทางตรง ทางโค้ง หรือหักเป็นมุมฉาก ระยะทางที่รถเคลื่อนที่อาจเป็นระยะทางตามตัวเลขที่ราบของการเคลื่อนที่ แต่หากบางครั้งเราจะพบว่า จุดปลายทางที่เราเดินทางห่างจากจุดต้นทางในแนวเส้นตรง หรือในแนวสายตาไม่มากนัก

ระยะทาง (distance) คือ ความยาวตามเส้นทางที่วัตถุเคลื่อนที่ไปได้ทั้งหมด เป็นปริมาณสเกลาร์ คือ มีแต่ขนาดอย่างเดียว มีหน่วยเป็นเมตร โดยทั่วไปเราใช้สัญลักษณ์ S

การกระจัด (displacement) คือ เส้นตรงที่เชื่อมโยงระหว่างจุดเริ่มต้น และจุดสุดท้ายของการเคลื่อนที่เป็นปริมาณเวกเตอร์ คือ ต้องคำนึงถึงทิศทางด้วย มีหน่วยเป็นเมตร โดยทั่วไปเขียนแบบเว็กเตอร์เป็น S

อัตราเร็ว

อัตราเร็ว (สัญลักษณ์: v) คืออัตราของ การเคลื่อนที่ หรือ อัตราการเปลี่ยนแปลงของตำแหน่งก็ได้ หลายครั้งมักเขียนในรูป ระยะทาง d ที่เคลื่อนที่ไปต่อ หน่วย ของ เวลา t

อัตราเร็ว เป็นปริมาณ สเกลาร์ที่มีมิติเป็นระยะทาง/เวลา ปริมาณเวกเตอร์ที่เทียบเท่ากับอัตราเร็วคือความเร็ว อัตราเร็ววัดในหน่วยเชิงกายภาพเดียวกับความเร็ว แต่อัตราเร็วไม่มีองค์ประกอบของทิศทางแบบที่ความเร็วมี อัตราเร็วจึงเป็นองค์ประกอบส่วนที่เป็นขนาดของความเร็ว

ในรูปสัญลักษณ์ทางคณิตศาสตร์ อัตราเร็วคือ

$v = \frac {d}{t}$

หน่วยของอัตราเร็ว ได้แก่

เมตรต่อวินาที, (สัญลักษณ์ m/s) , ระบบหน่วย SI
กิโลเมตรต่อชั่วโมง, (สัญลักษณ์ km/h)
ไมล์ต่อชั่วโมง, (สัญลักษณ์ mph)
นอต (ไมล์ทะเลต่อชั่วโมง, สัญลักษณ์ kt)
มัค เมื่อมัค 1 เท่ากับ อัตราเร็วเสียง มัค n เท่ากับ n เท่าของอัตราเร็วเสียง

มัค 1 ≈ 343 m/s ≈ 1235 km/h ≈ 768 mi/h (ดู อัตราเร็วเสียง สำหรับข้อมูลเพิ่มเติม)

อัตราเร็วแสง ใน สุญญากาศ (สัญลักษณ์ c) เป็นหนึ่งใน หน่วยธรรมชาติ

c = 299,792,458 m/s

การเปลี่ยนหน่วยที่สำคัญ

1 m/s = 3.6 km/h

1 mph = 1.609 km/h

1 knot = 1.852 km/h = 0.514 m/s

ยานพาหนะต่าง ๆ มักมี speedometer สำหรับวัดอัตราเร็ว

วัตถุที่เคลื่อนที่ไปตามแนวราบ พร้อม ๆ กับแนวดิ่ง (เช่น อากาศยาน) จะแยกประเภทเป็น forward speed กับ climbing speed

[แก้]
อัตราเร็วในรูป สมบัติเชิงกายภาพ มักแทนอัตราเร็วที่ขณะใดขณะหนึ่ง ในชีวิตจริงเรามันใช้ อัตราเร็วเฉลี่ย (ใช้สัญลักษณ์ $\tilde{v}$ ) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลา

อัตราเร็วเฉลี่ย

ยกตัวอย่างเช่น ถ้าคุณเคลื่อนที่ได้ 60 ไมล์ในเวลา 2 ชั่วโมง อัตราเร็ว เฉลี่ย ของคุณในช่วงเวลานั้นคือ 60/2 = 30 ไมล์ต่อชั่วโมง แต่อัตราเร็วที่ขณะใดขณหนึ่งย่อมเปลี่ยนแปลงต่างกันไป

ในรูปสัญลักษณ์ทางคณิตศาสตร์

$\tilde{v} = \frac{\Delta l}{\Delta t}.$

อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ เวลา ในช่วงเวลา $[t_0, t_1]$ จะให้อัตราเร็วเฉลี่ยในรูป

$\tilde{v} = \frac{\int_{t_0}^{t_1} v (t) \, dt}{\Delta t}$

ในขณะที่อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ ระยะทาง (หรือ ความยาว) ในช่วงความยาว $[l_0, l_1]$ จะให้อัตราเร็วเฉลี่ยในรูป

$\tilde{v} = \frac{\Delta l}{\int_{l_0}^{l_1} \frac{1}{v (l) } \, dl}$

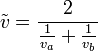
บ่อยครั้งที่มีคนคาดโดยสัญชาตญาณ แต่ผิด ว่าการเคลื่อนที่ครึ่งแรกของระยะทางด้วยอัตราเร็ว $v_{a}$ และระยะทางครึ่งที่สองด้วยอัตราเร็ว $v_{b}$ จะให้อัตราเร็วเฉลี่ยรวมเป็น $\tilde{v} = \frac{v_a + v_b}{2}$ ค่าที่ถูกต้องต้องเป็น $\tilde{v} = \frac{2}{\frac{1}{v_a} + \frac{1}{v_b}}$
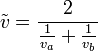
(ระลึกไว้ว่า อย่างแรกเป็น ค่าเฉลี่ยเลขคณิต ในขณะที่อย่างที่สองเป็น ค่าเฉลี่ยฮาร์มอนิก)

อัตราเร็วเฉลี่ยสามารถหาได้จาก distribution function ของอัตราเร็วได้เช่นกัน (ทั้งในรูประยะทางหรือเวลาก็ตาม)

$v \sim D_t\; \Rightarrow \; \tilde{v} = \int v D_t (v) \, dv$

$v \sim D_l\; \Rightarrow \; \tilde{v} = \frac{1}{\int \frac{D_l (v) }{v} \, dv}$

[แก้]นัยสำคัญทางวัฒนธรรม

อัตราเร็วหรือ ความว่องไวของการเคลื่อนที่มีบทบาทสำคัญในวัฒนธรรมของมนุษย์และสัตว์ (ดู การแข่งความเร็ว) มันเป็นองค์ประกอบของ ความนุ่มนวล ความแม่นยำ และ ความแข็งแกร่ง เช่น ในการเต้นรำ หรือ ศิลปะการรบ สัตว์ที่เป็นสัญลักษณ์ของอัตราเร็วคือ ม้า (PIE *ek'vos มีที่มาจากคำว่า *ok'u- "ว่องไว") นก โดยเฉพาะนกนักล่าอย่าง เหยี่ยว และแมว คือ lynx (ดู Flos Duellatorum) สัตว์บกที่รวดเร็วที่สุดคือ ชีต้า ซึ่งมีอัตราเร็วในการวิ่งถึง 110 km/h (68 mph) ในระยะทางสั้น ๆ สำหรับอัตราเร็วสม่ำเสมอแล้ว สัตว์บกที่เร็วที่สุดก็คือ ม้าพันธุ์ดีที่ได้รับการฝึก

[แก้]อัตราเร็วทั่วไปของวัตถุซึ่งเคลื่อนที่

สำหรับมนุษย์ อัตราเร็วของ การเดิน ของมนุษย์อยู่ที่ประมาณ (~5 km/h, 1.39 m/s) ถึงแม้ว่ามันจะขึ้นอยู่กับปัจจัยหลายอย่าง เช่น ความสูง น้ำหนัก และอายุ
การวิ่ง: อัตราเร็วสำหรับระยะทางไกล การจ้อกกิ้ง สำหรับคนโดยเฉลี่ยอยู่ที่ประมาณ 6 mph (~10 km/h, 2.7 m/s) นักกีฬาชั้นยอดสามารถวิ่งเต็มเหยียดด้วยอัตราเร็ว 23.03 mph (~36.85 km/h, 10.24 m/s) ภายในระยะทางสั้น ๆ เช่น การวิ่ง 200 เมตร
การขี่จักรยาน: 12 mph (~20 km/h, 5.56 m/s)
รถยนต์: โดยเฉลี่ย 65 mph (~104 km/h, 28.9 m/s ) บนทางด่วน

ความเร็ว

ในทางฟิสิกส์ ความเร็ว คืออัตราการเปลี่ยนแปลงของตำแหน่งต่อหน่วยเวลา มีหน่วยเป็นเมตรต่อวินาที (m/s) ในหน่วยเอสไอ ความเร็วเป็นปริมาณเวกเตอร์ซึ่งประกอบด้วยอัตราเร็วและทิศทาง ขนาดของความเร็วคืออัตราเร็วซึ่งเป็นปริมาณสเกลาร์ ตัวอย่างเช่น "5 เมตรต่อวินาที" เป็นอัตราเร็ว ในขณะที่ "5 เมตรต่อวินาทีไปทางทิศตะวันออก" เป็นความเร็ว ความเร็วเฉลี่ย v ของวัตถุที่เคลื่อนที่ไปด้วยการกระจัดขนาดหนึ่ง ∆x ในช่วงเวลาหนึ่ง ∆t สามารถอธิบายได้ด้วยสูตรนี้

$\mathbf{\bar{v}} = \frac{\Delta \mathbf{x}}{\Delta t}$

อัตราการเปลี่ยนแปลงของความเร็วคือความเร่ง คือการอธิบายว่าอัตราเร็วและทิศทางของวัตถุเปลี่ยนไปอย่างไรในช่วงเวลาหนึ่ง และเปลี่ยนไปอย่างไร ณ เวลาหนึ่ง

[แก้]สมการการเคลื่อนที่

ดูบทความหลักที่ สมการการเคลื่อนที่

เวกเตอร์ความเร็วขณะหนึ่ง v ของวัตถุที่มีตำแหน่ง x (t) ณ เวลา t และตำแหน่ง x (t + ∆t) ณ เวลา t + ∆t สามารถคำนวณได้จากอนุพันธ์ของตำแหน่ง

$\mathbf{v} = \lim_{\Delta t \to 0}{{\mathbf{x}(t+\Delta t)-\mathbf{x}(t)} \over \Delta t} = {\mathrm{d}\mathbf{x} \over \mathrm{d}t}$

สมการของความเร็วของวัตถุยังสามารถหาได้จากปริพันธ์ของสมการของความเร่ง ที่วัตถุเคลื่อนที่ตั้งแต่เวลา t₀ ไปยังเวลา t_n

วัตถุที่มีความเร็วเริ่มต้นเป็น u มีความเร็วสุดท้ายเป็น v และมีความเร่งคงตัว a ในช่วงเวลาหนึ่ง ∆t ความเร็วสุดท้ายหาได้จาก

$\mathbf{v} = \mathbf{u} + \mathbf{a} \Delta t$

ความเร็วเฉลี่ยอันเกิดจากความความเร่งคงตัวจึงเป็น $\tfrac {(\mathbf{u} + \mathbf{v})}{2}$ ตำแหน่ง x ที่เปลี่ยนไปของวัตถุดังกล่าวในช่วงเวลานั้นหาได้จาก

$\Delta \mathbf{x} = \frac {( \mathbf{u} + \mathbf{v} )}{2} \Delta t$

กรณีที่ทราบเพียงความเร็วเริ่มต้นของวัตถุเพียงอย่างเดียว คำนวณได้ดังนี้

$\Delta \mathbf{x} = \mathbf{u} \Delta t + \frac{1}{2}\mathbf{a} \Delta t^2$

และเมื่อต้องการหาตำแหน่ง ณ เวลา t ใด ๆ ก็สามารถขยายนิพจน์ได้ดังนี้

$\mathbf{x}(t) = \mathbf{x}(0) + \Delta \mathbf{x} = \mathbf{x}(0) + \mathbf{u} \Delta t + \frac{1}{2}\mathbf{a} \Delta t^2$

อัตราเร่ง
เป็นสมรรถนะของรถยนต์ที่มีความสำคัญและเกี่ยวข้องกัน แต่ผู้ขับบางคนยังขาดความเข้าใจที่ถูกต้อง โดยมักพุ่งความสนใจไปที่ความเร็วเพียงอย่างเดียว โดยไม่ได้สนใจอัตราเร่ง ทั้งที่มีความสำคัญไม่แพ้กัน เพราะต้องใช้ตลอดการขับ

จากสภาพการจราจรที่ติดขัดมากขึ้นทุกขณะ ทำให้ผู้ขับบางคนคิดว่า เครื่องยนต์สมรรถนะสูงไม่มีความจำเป็นสำหรับการใช้งานทั่วไปเพราะไม่มีโอกาสขับด้วยความเร็วสูง โดยจะให้ความสำคัญกับความเร็วก็ต่อเมื่อใช้งานในต่างจังหวัดหรือเดินทางไกลเท่านั้น แต่มองข้ามเรื่องอัตราเร่ง ตั้งแต่ขั้นตอนการเลือกซื้อรถยนต์จนถึงการใช้งานจริงทั้งที่เป็นสมรรถนะของรถยนต์ที่ควรให้ความสนใจ เพราะต้องใช้งานทุกวินาทีที่รถยนต์เคลื่อนที่ ตั้งแต่การออกตัวจากจุดหยุดนิ่ง, ช่วงความเร็วปานกลาง และช่วงความเร็วสูง

อัตราเร่ง
หมายถึง การเพิ่มความเร็ว จากความเร็วหนึ่ง ไปยังอีกความเร็วหนึ่งที่สูงขึ้น เช่น อัตราเร่งจากความเร็ว 40 กิโลเมตร/ชั่วโมง ไปยังความเร็ว 80 กิโลเมตร/ชั่วโมง หรือตามมาตรฐานการทดสอบที่นิยมกัน คือ จากจุดหยุดนิ่งไปยังความเร็ว 100 กิโลเมตร/ชั่วโมง

อัตราเร่ง มีความเกี่ยวเนื่องกับความเร็ว รถยนต์ที่มีอัตราเร่งดี คือ สามารถเพิ่มความเร็วโดยใช้เวลาและระยะทางสั้นในทุกช่วงความเร็ว

ความเร็ว
หมายถึง ความสามารถในการเคลื่อนที่ของรถยนต์ มีหน่วยเป็นระยะทาง/เวลา เป็นอีกหนึ่งพื้นฐานหลักในการใช้รถยนต์เทคโนโลยีมากมายที่ถูกผสานเข้าไปในรถยนต์ เพื่อเอาชนะแรงดึงดูดของโลก ทำให้รถยนต์ยุคใหม่สามารถทำความเร็วได้สูงขึ้น

การใช้ความเร็วสูงสุดอย่างปลอดภัยมีองค์ประกอบหลายอย่าง เช่น ความพร้อมของผู้ขับและรถยนต์ สภาพถนนหรือการจราจรรวมทั้งสภาพแวดล้อมในขณะนั้นด้วย จึงมีโอกาสได้ใช้น้อย

ส่วนอัตราเร่งไม่จำเป็นต้องใช้เฉพาะช่วงความเร็วสูงเท่านั้น แต่สามารถใช้ได้ตลอดเวลาหรือทุกครั้งที่กดคันเร่ง เช่นการออกตัวเมื่อได้สัญญาณไฟเขียว และการเปลี่ยนเลนหรือลัดเลาะไปตามสภาพการจราจรที่แออัด
อัตราเร่งมีส่วนเกี่ยวข้องกับความปลอดภัย รถยนต์ที่มีอัตราเร่งดีหรือที่เรียกกันว่า ขึ้นเร็ว จะมีความปลอดภัยในหลายสถานการณ์ เช่นการเปลี่ยนจากทางขนานเข้าสู่ทางด่วน ที่ต้องเร่งความเร็ว ให้ใกล้เคียงกับรถยนต์ที่อยู่ในทางด่วน หรือการแซงบนถนน 2 เลนหากเป็นรถยนต์ที่มีอัตราเร่งไม่ดีหรือ ขึ้นช้า ก็อาจทำให้เกิดอุบัติเหตุได้

ความเร่ง

ในฟิสิกส์ ความเร่ง (อังกฤษ: acceleration, สัญลักษณ์: a) คือ อัตราการเปลี่ยนแปลง (หรืออนุพันธ์เวลา) ของความเร็ว เป็นปริมาณเวกเตอร์ที่มีหน่วยเป็น ความยาว/เวลา² ในหน่วยเอสไอกำหนดให้หน่วยเป็น เมตร/วินาที²

เมื่อวัตถุมีความเร่งในช่วงเวลาหนึ่ง ความเร็วของมันจะเปลี่ยนแปลงไป ความเร่งอาจมีค่าเป็นบวกหรือลบก็ได้ ซึ่งเรามักว่าเรียกความเร่ง กับความหน่วง ตามลำดับ ความเร่งมีนิยามว่า "อัตราการเปลี่ยนแปลงความเร็วของวัตถุในช่วงเวลาหนึ่ง" และกำหนดโดยสมการนี้

$\mathbf{a} = {d\mathbf{v}\over dt}$

เมื่อ

a คือ เวกเตอร์ความเร่ง

v คือ เวกเตอร์ความเร็ว ในหน่วย m/s

t คือ เวลา ในหน่วยวินาที

จากสมการนี้ a จะมีหน่วยเป็น m/s² (อ่านว่า "เมตรต่อวินาทียกกำลังสอง")

หรือเขียนเป็นอีกสมการได้

$\mathbf{\bar{a}} = {\mathbf{v} - \mathbf{u} \over t}$

เมื่อ

$\mathbf{\bar{a}}$ คือ ความเร่งเฉลี่ย (m/s²)

$\mathbf{u}$ คือ ความเร็วต้น (m/s)

$\mathbf{v}$ คือ ความเร็วปลาย (m/s)

$\mathbf{t}$ คือ ช่วงเวลา (s)

การหาค่าความชันของกราฟ

ความชันจะหาได้จาก
1.สมการที่กำหนดมาเเล้ว
2.จุด 2 จุดที่เส้นกราฟผ่าน

จาก1.

เช่น y = 2x+1
ได้ความชัน 2 ระยะตัดเเกน y 1
ความชันได้มาจากหน้า x ถ้าไม่มีเลยเช่น y = x+9
เเสดงว่ามการนี้มีความชัน 1

จาก 2

สมมติมีจุดตัดมาให้ 2 จุดเช่น
(3,6)เเละ(4,8)
หาได้ทั้งความชันเเละสมการโดย
หาความชันได้จากการนำค่า y จากพิกัดที่กำหนดคือพจน์หลังของทั้ง 2
พิกัด มาลบกันเเล้วนำค่าทั้งหมดที่ได้หารด้วย ค่าของ x ในพิกัดทั้งสอง
มาลบกัน ตามตัวอย่างได้
(8 - 6) / (4-3) ได้ 2 ความชันได้ 2

กราฟความสัมพันธ์ระหว่าง s-t, v-t และ a-t

กราฟความสัมพันธ์ระหว่าง s-t

สิ่งที่สามารถหาได้จากกราฟการกระจัดและเวลา คือ ความเร็วเฉลี่ย อัตราเร็วเฉลี่ย และความเร็วขณะใดๆ โดยแยกพิจารณาได้ดังนี้
ระยะทาง (s) คือ ความยาวตามเส้นทางที่อนุภาคเคลื่อนที่ผ่าน
ความเร็วเฉลี่ย และความเร็วเฉลี่ย(v ) หาได้จากสมการ [ A av = s/t]
ความเร็วขณะใดๆ หาได้จาก [v = ds/dt = ความชันของกราฟ s กับ t]

              
 
       ไม่มีการเคลื่อนที่                                      มีการเคลื่อนที่ โดย v คงที่

กราฟความสัมพันธ์ระหว่าง v-t

เราพิจารณาค่าต่างๆ จากกราฟได้ดังนี้

1.ความชันของกราฟ v กับ t คือความเร่งของวัตถุ slope v/t = a

2.พื้นที่ใต้กราฟของ v กับ t คือการกระจัดหรือระยะทาง พื้นที่ใต้กราฟ = vt = s

3.ส่วนตัดแกน y คือ ความเร็วต้น

ข้อควรจำ
ถ้ากราฟความสัมพันธ์ระหว่าง v กับ t มีทั้งบวกและลบ เราแยกพิจารณาได้ดังนี้

- ระยะทาง มีค่าเท่ากับผลรวมของพื้นที่ใต้กราฟ v - t โดยไม่คิดเครื่องหมาย

- การกระจัด มีค่าเท่ากับผลรวมของพื้นที่ใต้กราฟ v - t โดยคิดเครื่องหมายพื้นที่ด้วย

       

     มีการเคลื่อนที่ด้วย v  คงที่                   มีการเคลื่อนที่ด้วย a คงที่               พื้นที่ใต้กราฟ  คือการกระจัด

กราฟความสัมพันธ์ระหว่าง a-t

กราฟความสัมพันธ์ระหว่างความเร่งกับเวลา เราสามารถคำนวณหาความเร็วขณะใดๆ และการกระจัดหรือระยะทาง โดยแยกการพิจารณาได้ดังนี้

1)ถ้าต้องการหาความเร็วขณะใดๆ ให้คำนวณจากกราฟ กับ a ได้เลย t จะได้
v - u = พื้นที่ใต้กราฟ a กับ t
โดย v = ความเร็วปลาย และ u = ความเร็วต้น

2) ถ้าต้องการหาระยะทางหรือการกระจัด ให้แปลงกราฟ a กับ t เป็นกราฟ v กับ t เสียก่อน แล้วจึงค่อยคำนวณหาการกระจัด หรือระยะทางจากพื้นที่ใต้กราฟ v กับ t

การหาความเร็วและความเร่งจากกราฟ

ความเร่ง คือ ความเร็วที่เปลี่ยนไปในหนึ่งหน่วยเวลา หรือ อัตราการเปลี่ยนแปลงความเร็วเป็นปริมาณ เวคเตอร์

หรือ

= ${vec{v_2} - vec{v_1}}/{{t_2} - {t_1}}$

เราสามารถหาค่าของความเร่งได้จากความชัน(slope)

ถ้าข้อมูลให้เป็นกราฟ ความเร็ว กับ เวลา (v-t)

ความเร่งขณะหนึง คือ ความเร่งในช่วงเวลาสั้นๆในกรณีที่เราหาความเร่ง เมื่อ t เข้าใกล้ศูนย์ ความเร่งขณะนั้นเราเรียกว่า ความเร่งขณะหนึ่ง ถ้าข้อมูลเป็นกราฟ หาได้จาก slope ของเส้นสัมผัส

ความเร่งเฉลี่ย คือ อัตราส่วนระหว่างความเร็วที่เปลี่ยนไปทั้งหมดกับช่วงเวลาที่เปลี่ยนความเร็วนั้น

กราฟแสดงความสัมพันธ์ระหว่างความเร่ง (a) กับเวลา (t)

สามารถหาความเร็วได้โดย

= พื้นที่ใต้กราฟ

${v_2} - {v_1}$ = พื้นที่ใต้กราฟ

ข้อสังเกต

1 วัตถุที่เคลื่อนที่ด้วยความเร่ง วัตถุจะเคลื่นที่เร็วขึ้นเมื่อเวลาผ่าน

2 วัตถุเคลื่อนที่ด้วยความเร็วคงที่ วัตถุเคลื่อนที่ด้วยเร็วคงตัวตลอดการเคลื่อนที่

3 วัตถุเคลื่อนที่ด้วยความหน่วง วัตถุเคลื่อนที่ช้าลงเมื่อเวลาผ่านไป

ตัวอย่างการคำนวณ

1 อนุภาคหนึ่งมีความเร็วของอนุภาคสัมพันธ์กับเวลาดังรูป จงหาความเร่งช่องเวลา 2-6 วินาที

คิดวิเคราะห์ : กราฟระหว่งความเร็ว (v) กับเวลา (t) หาความเร่งได้จากความชันของกราฟ

กราฟระหว่างความเร็ว (v) กับเวลา (t) หาความเร่งได้จากความชันของกราฟ

วิธีทำ จาก ความเร่ง = ความชันของกราฟช่วง 2 – 6 วินาที

= ${{v_2} - {v_1}}/{{t_2} - {t_1}}$

= 0.5 เมตร/วินาที²

ความหน่วง (Deceleration)

คือความเร่งที่มีทิศตรงข้ามกับการเคลื่อนที่ ความหน่วงจึงมีเครื่องหมายเป็นลบ

สำหรับการเรียนในชั้นนี้ เราจะเรียนเฉพาะกรณีความเร่งหรือความหน่วงคงที่เท่านั้น กราฟความเร่งจึงไม่ค่อยได้พบเท่าใดนัก

ความเร็ว

คืออัตราการเปลี่ยนแปลงการขจัด เป็นปริมาณเวคเตอร์ แบ่งการพิจารณาได้เป็น 2 แบบคือ

1ความเร็วใดๆ (เราใช้สัญลักษณ์ vec{v}

)คือความเร็วที่เกิดขึ้น ณ เวลาใดเวลาหนึ่งของการเคลื่อนที่ หรือคืออัตราการเปลี่ยนแปลงเวลาสั้นมากๆ เราสามารถเขียนในความสัมพันธ์ของสมการได้

ซึ่งความหมายของ ds/dt

ก็คือค่า slop ของกราฟ vec{s}

กับ t ในทางคณิตศาสตร์นั้นเอง

2 ความเร็วเฉลี่ย (Average Velocity ) ใช้สัญลักษณ์ $vec{v}_av$ คืออัตราส่วนของการขจัดต่อเวลา เมื่อการเปี่ยนแปลงเวลาอยู่ในช่วงยาวเป็นปริมาณเวคเตอร์ ซึ่งเขียนในความสัมพันธ์ได้

อัตราเร็ว(Speed)

คือ อัตราการเปลี่ยนแปลงระยะทางเป็นปริมาณสเกวลาร์ แยกการพิจารณาได้เป็น 2 แบบคือ 1 อัตราเร็วขณะใดๆ(v) คืออัตราส่วนของระยะทางต่อเวลาเมื่อการเปลี่ยนแปลงเวลาอยู่ในช่วงสั้นๆ อัตราเร็วใดๆ จะมีขนาดเท่ากับขนาดของความเร็วขณะนั้นๆ ซึ่งเขียนในความสัมพัมธ์ได้

2 อัตราเร็วเฉลี่ย ${v_av}$ คืออัตราส่วนของระยะทางต่อเวลาเมื่การเปลี่ยนแปลงเวลาอยู่ช่วงยาว เขียนในความสัมพัมธ์ได้

หมายเหตุ 1 อัตราเร็วขณะใดๆ ก็คือขนาดของความเร็วขณะนั้นๆ เสมอ

2 อัตราเร็วเฉลี่ยจะมีค่าเท่ากับความเร็วเฉลี่ยในกรณีที่วัตถุเคลื่อนที่ในแนวเส้นตรงที่ไม่มีการถอยหลังกลับเท่านั้น

กราฟความสัมพันธ์ระหว่างความเร็ว(v) และ เวลา (t)

1. กราฟระหว่าง การกระจัด(S) - เวลา(t) ความชันของกราฟนี้คือ ความเร็ว
ถ้าเปลี่ยนเป็นกราฟ ความเร็ว(V ) - เวลา(t) ก็เปลี่ยนจากความชัน

2. กราฟระหว่าง ความเร็ว(V ) - เวลา(t) ความชันของกราฟนี้คือ ความเร่ง
ถ้าเปลี่ยนเป็นกราฟ ความเร่ง(a) - เวลา(t) ก็เปลี่ยนจากความชัน

สมการการเคลื่อนที่ในแนวตรงด้วยความเร่งคงที่

การเคลื่อนที่ ในแนวตรง

อัตราเร็ว คือการเปลี่ยนแปลง ระยะทาง ต่อเวลา

อัตราเร็วเฉลี่ย หน่วย เมตร/วินาที(m/s)

s = ระยะทางที่เคลื่อนที่ได้ (m) ตามแนวเคลื่อนที่จริง

t = เวลาในการเคลื่อนที่ (s)

ความเร็ว คือ การเปลี่ยน แปลงการกระจัด

ความเร็วเฉลี่ย หน่วย เมตร/วินาที (m/s)

s = การกระจัด (m) คือ ระยะทางที่สั้นที่สุดในการย้ายตำแหน่ง หนึ่งไป อีกตำแหน่งหนึ่ง

ความเร่ง คือ อัตราการเปลี่ยน ความเร็ว

ความเร่ง หน่วย เมตรต่อ วินาที²( m/s²)

a = ความเร่ง

แสดง เป็นกราฟ

การกระจัดกับเวลา	ความเร็วกับเวลา	ความเร่งกับเวลา

การเคลื่อนที่ในแนวเส้นตรง

การเคลื่อนที่ในแนวตรงด้วยความเร่งคงที่ มีสูตรดังนี้

s = vt

u = ความเร็วเริ่มต้น (m/s)
v = ความเร็วตอนปลาย (m/s )
s = ระยะทาง(m)
a = ความเร่ง ( m/s²)

การเคลื่อนที่ในแนวดิ่งภายใต้แรงดึงดูดของโลก

1.v = u - gt

u = ความเร็วต้น เป็น + เสมอ

v = ความเร็วปลาย + ถ้าทิศเดียวกับ u และเป็น - ถ้าทิศตรงขามกับ u
s หรือ h = ระยะทางเป็น + ตอนวิ่งขึ้น และเป็น - ตอนวิ่งลง

3.v² = u ²+2gh

g = ความเร่งจากแรงโน้มถ่วง

สมการการเคลื่อนที่แนวดิ่งด้วยความเร่งคงที่

เป็นการเคลื่อนที่ของวัตถุที่ตกอย่างอิสระภายใต้แรงโน้มถ่วงของโลกเพียงแรงเดียว การเคลื่อนที่ลักษณะนี้จะไม่คิดแรงต้านของอากาศ
การตกอย่างอิสระวัตถุจะเคลื่อนที่ด้วยความเร่งค่าหนึ่ง เรียกว่า ความเร่งโน้มถ่วง (Gravitational acceleration) เขียนแทนด้วย g ซึ่งมีค่าประมาณ 9.8 m/s²

สมการการเคลื่อนที่ในแนวดิ่ง เนื่องจากการเคลื่อนที่ในแนวดิ่ง คือ การการเคลื่อนที่ในแนวเส้นตรงแบบหนึ่ง ดังนั้น สมการในการคำนวณจึงเหมือนกับสมการการเคลื่อนที่ในแนวราบเพียงแต่เปลี่ยนค่า a เป็นg เท่านั้น

	u คือ ความเร็วต้น (m/s) v คือ ความเร็วปลาย (m/s) g คือ ความเร่ง (m/s²) t คือ เวลา (s) s คือ การกระจัด (m)

การคำนวณการเคลื่อนที่ของวัตถุภายใต้แรงดึงดูดของโลก

กาลิเลโอ ได้ทำการทดลองให้เห็นว่า วัตถุที่ตกลงสู่พื้นโลกอย่างอิสระ จะเคลื่อนที่ภายใต้แรงดึงดูดของโลก ต่อมานิวตันสังเกตุเห็นว่า ทำไมดวงจันทร์ไม่ลอยหลุดออกไปจากโลก ทำไมผลแอปเปิ้ลจึงตกลงสู่พื้นดิน นิวตันได้ทำการศึกษาค้นคว้าต่อ จนในที่สุดก็สามารถพิสูจน์ในเรื่องกฎแห่งการดึงดูดของ สสาร โดยโลกและดวงจันทร์ต่างมีแรงดึงดูดซึ่งกันและ กัน แต่เนื่องจากดวงจันทร์โคจรรอบโลก จึงมีแรงหนีสู่ศูนย์กลางซึ่งต่อต้านแรงดึงดูดไว้ ทำให้ดวงจันทร์ลอยโคจรรอบโลกได้ แต่ผลแอปเปิ้ลกับโลกก็มีแรงดึงดูดระหว่างกัน ผลแอปเปิ้ลเมื่อหลุดจากขั้วจึงเคลื่อนที่อิสระตามแรงดึงดูดนั้น

การตกอย่างอิสระนี้ วัตถุจะเคลื่อนตัวด้วยความเร่ง ซึ่งเรียกว่า Gravitational acceleration หรือ g ซึ่งมีค่าประมาณ 9.8 m/s

การเคลื่อนที่ในแนวดิ่งนี้จึงเป็นไปตาม กฎการเคลื่อนที่ ดังนี้

ตัวอย่างเช่น ขว้างหินจากชั้น 4 ของตึกขึ้นไปในแนวดิ่ง ด้วยความเร็ว 10 m/s ณ จุดที่มีความสูง 14 เมตร จงหาว่าก้อนหินใช้เวลาอยู่ในอากาศนานเท่าใดจึง ตกถึงพื้น และความเร็วขณะถึงพื้นเป็นเท่าใด

ระยะทาง

จากการคำนวณหาความเร็วสุดท้าย
แทนค่าได้

เมื่อทราบความเร็วต้น และความเร็วสุดท้าย

ความเร็วต้นมีทิศเป็นลบ
ความเร็วปลายมีทิศเป็นบวก
อัตราเร่ง g มีทิศตรงข้ามกับทิศทางที่ขว้าง จึงมีค่าเป็นลบ

ความเร็วสัมพัทธ์(Relative Velocity)

เราคงเคยสังเกตความเร็วของรถที่วิ่งสวนทางกับรถที่เรานั่งอยู่ หรือความเร็วของรถคันที่รถเราวิ่งแซงนะครับ ซึ่งเราจะพบว่า ความเร็วของรถที่วิ่งสวนทางเราดูเหมือนจะมีความเร็วสูงเป็นพิเศษ แต่ความเร็วของรถคันที่ถูกเราแซงกลับมีความเร็วที่ช้าผิดปกติ เราอาจจะสงสัยว่าเอะ! เกิดอะไรขึ้น...ปรากฎการณ์ความเร็วที่เปลี่ยนไปนี้ เราเรียกว่า ความเร็วสัมพัทธ์ (Relative Velocity) ลองดูตัวอย่างเหตุการณ์นี้ครับ...

XXXXXXXจากภาพ เราสามารถบอกได้ว่า รถ B วิ่งแซงหน้ารถ A และคนขับรถ B สังเกตเห็นรถ A วิ่งด้วยความเร็ว «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mo»-«/mo»«mn»5«/mn»«mo»§nbsp;«/mo»«mi»m«/mi»«mo»/«/mo»«mi»s«/mi»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mo»-«/mo»«mn»5«/mn»«mo»§nbsp;«/mo»«mi»m«/mi»«mo»/«/mo»«mi»s«/mi»«/math»

นั่นคือ รถ A วิ่งห่างออกไปข้างหลังรถ B เราเรียกว่า ความเร็ว A สัมพัทธ์กับ B ( «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

) ในทางตรงข้ามกัน คนขับรถ A จะสังเกตเห็นรถ B วิ่งด้วยความเร็ว «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mn»5«/mn»«mo»§nbsp;«/mo»«mi»m«/mi»«mo»/«/mo»«mi»s«/mi»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mn»5«/mn»«mo»§nbsp;«/mo»«mi»m«/mi»«mo»/«/mo»«mi»s«/mi»«/math»

นั่นคือ รถ B วิ่งแซงหน้าไปด้วยความเร็ว 5 m/s เราเรียกว่า ความเร็ว B สัมพัทธ์กับ A ( «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»BA«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»BA«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

)

XXXXXXXจากภาพ เหตุการณ์ที่สอง เราสามารถบอกได้ว่า รถ B วิ่งสวนทางกับรถ A และคนขับรถ B สังเกตเห็นรถ A วิ่งสวนทางไปด้วยความเร็ว

นั่นคือ รถ A วิ่งสวนทางไปข้างหลัง (เครื่องหมายติดลบ -) รถ B ด้วยความเร็วขนาด 25 เมตรต่อวินาที และเราเรียกว่า ความเร็ว A สัมพัทธ์กับ B ( «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

) ในทำนองเดียวกัน คนขับรถ A ก็จะเห็นรถ B วิ่งด้วยความเร็วเดียวกันนี้แต่ทิศตรงข้ามกัน

XXXXXXXเพื่อให้เข้าใจยิ่งขึ้น เราสามารถสรุปได้ว่า การหาความเร็วสัมพัทธ์ ในกรณีที่วัตถุเคลื่อนที่ไปทิศทางเดียวกัน หรือสวนทางกัน หาได้จาก “ความเร็วของวัตถุ – ความเร็วของผู้สังเกต” เขียนเป็นสมการได้ว่า

XXXXXXXXXXXXXXXXXXXXX «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»=«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«mo»-«/mo»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»B«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

XXXXXXXเมื่อ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»AB«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

เป็นความเร็วของวัตถุ A สัมพัทธ์กับ B

XXXXXXXXXXXX «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»v«/mi»«mi»A«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

เป็นความเร็วของวัตถุ A สัมพัทธ์กับกรอบอ้างอิงเฉื่อย

XXXXXXXXXXXX «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover accent=¨true¨»«msub»«mi»V«/mi»«mi»b«/mi»«/msub»«mo»§#8594;«/mo»«/mover»«/math»

เป็นความเร็วของวัตถุ B สัมพัทธ์กับกรอบอ้างอิงเฉื่อย

การเคลื่อนที่ในสองมิติ และสามมิติ

การเคลื่อนที่ในสองมิติสามารถแยกคิดแบบการเคลื่อนที่หนึ่งมิติที่ตั้งฉากกัน และสามารถ นำการคิดสองทางนั้นมาประกอบกันหรือนำมารวมกันแบบเวกเตอร์ได้ ตามแนวของแกนสามแกนที่ ตั้งฉากซึ่งกัน คือ ตามแกนของระบบโคออร์ดิเนต XYZ สำหรับการเคลื่อนที่สามมิติ และตามแกน ของระบบโคออร์ดิเนต XY สำหรับการเคลื่อน ที่สองมิติ ตำแหน่งของวัตถุในสองมิติที่จุด P ที่เวลา

กำหนดได้ด้วยค่า

และ

ทางแกน X และแกน Y ตามลำดับ และตำแหน่งของวัตถุนั้นที่เวลา

(จุด Q) สมมติ
ให้เป็น

และ

การกระจัดหรือการเปลี่ยนแปลงตำแหน่งระหว่างสองจุดนั้นให้เป็น ไปตามเส้นโค้งดังรูป

รูป แสดงตำแหน่งและการกระจัดของวัตถุในช่วงเวลา

กับ

ความเร็วเฉลี่ยสำหรับการเคลื่อนที่ทาง X คือ

และความเร็วเฉลี่ยสำหรับการเคลื่อนที่ทาง Y คือ

เมื่อ

กับ

เข้าใกล้กันมาก ๆ ความเร็วเฉลี่ยก็จะเป็นความเร็วขณะใดขณะหนึ่งเช่นเดียวกับการคิดในหนึ่งมิติ

เวกเตอร์ตำแหน่งและเวกเตอร์ความเร็วในสองมิติ

= u

+ 2gs
v

= (10)

+ 2(-9.81) x (-14) = 374.7
v = 19.36

ดังตัวอย่างการเคลื่อนที่ที่ผ่านมา อาจคิดว่า เวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _1$ เป็นเวกเตอร์ตำแหน่ง (position vector) ที่เวลา $\displaystyle t_1$ สำหรับวัตถุที่มีค่าทาง x เป็น $\displaystyle x_1$ และมีค่า y เป็น $\displaystyle y_1$ เวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _1$ จะมีขนาดและทิศชัดเจนเทียบกับจุดกำเนิดของโคออร์ดิเนต เมื่อเวลาเปลี่ยนเป็น $\displaystyle t_2$ ตำแหน่งของวัตถุเปลี่ยนไปเป็นเวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} <br /> \over R} _2$

องค์ประกอบทาง x ของเวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _1$ คือ $\displaystyle x_1$ องค์ประกอบทาง y ของเวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _1$ คือ ค่า $\displaystyle y_1$ องค์ประกอบทาง x ของเวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _2$ คือ $\displaystyle x_2$ และองค์ประกอบทาง y ของเวกเตอร์ $\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _2$ คือ $\displaystyle y_2$
ความเร็วเฉลี่ยสามารถเขียนในรูปเวกเตอร์ได้เป็น

$\displaystyle \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _{av} = \frac{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _2 - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R} _1 }}{{t_2 - t_1 }}$

                 โดยมีองค์ประกอบทาง x และ y เป็นไปตามที่ได้เขียนมาแล้ว

                อัตราเร็วเฉลี่ย สำหรับการเคลื่อนที่ในสองมิติเช่นนี้ จะต่างจากความเร็วเฉลี่ยอย่างเห็นได้ชัดคือ ขนาดของอัตราเร็วเฉลี่ยระหว่างจุด P และ Q จะต้องคิดมาจากระยะทางตามเส้นโค้งตามเส้นทางของการเคลื่อนที่หารด้วยเวลา ในขณะที่ขนาดของความเร็วเฉลี่ยจะเป็นระยะทางตามเส้นตรงระหว่าง P และ Qหารด้วยเวลา ดังนั้น หากการเคลื่อนที่เป็นไปตามกราฟในรูป 2.6 อัตราเร็วเฉลี่ยจะมีค่ามากกว่าขนาดของความเร็วเฉลี่ย แต่เมื่อพิจารณาจุด P และ Q ที่เข้าใกล้กันมากขึ้น อัตราเร็วที่จุด Q ซึ่งเป็นอัตราเร็วที่ขณะใดขณะหนึ่ง จะมีขนาดเท่ากับขนาดของความเร็วขณะใดฯหนึ่งที่จุด Q นั่นเอง อัตราเร็วที่จุด Q ไม่จำเป็นต้องบอกทิศของการเคลื่อนที่ หรือไม่ใส่ใจเรื่องทิศว่ากำลังเคลื่อนที่ไปทางใด ส่วนความเร็วที่จุด Q จะต้องกำหนดหรือรู้ชัดว่ากำลังเคลื่อนที่ไปทางทิศใดด้วย

                 นักเรียนจะได้เรียนเรื่องทฤษฎีจลน์ของแก๊สในบทหนึ่งข้างหน้า ซึ่งจะได้ภาพว่าโมเลกุลของแก๊สในภาชนะปิดลอยอยู่ห่างๆกัน ไม่มีโมเลกุลที่อยู่นั่ง ทุกโมเลกุลเคลื่อนที่อยู่ตลอดเวลาด้วยอัตราเร็วต่างๆกัน และเคลื่อนที่ในทิศทางต่างๆ โดยมีความสมมาตร (symmetry) เชิงทิศทาง นั่นคือ ความเร็วที่ไปในทิศใดทิศหนึ่งก็เหมือนกับความเร็วที่ไปในทิศอื่นๆโดยรอบ ทำให้ความเร็วเฉลี่ยในทุกโมเลกุล (เป็นการเฉลี่ยระหว่างหลายๆโมเลกุลแทนที่จะเป็นการเฉลี่ยในช่วงเวลาที่ยาวขึ้น) มีค่าเป็นศูนย์ (ทำให้แก๊สทั้งหมดไม่ได้เคลื่อนที่ไปทางใด) แต่อัตราเร็วเฉลี่ยของโมเลกุลของแก๊สนี้จะไม่เป็นศูนย์ หรือการเฉลี่ยเฉเพาะขนาดของความเร็วโดยไม่คิดทิศ (ไม่เฉลี่ยแบบเวกเตอร์) จะไม่เป็นศูนย์ ดังนั้นจึงควรใช้คำอัตราเร็วเฉลี่ยของโมเลกุลซึ่งไม่เกี่ยวกับทิศของการเคลื่อนที่ของโมเลกุล

                 สำหรับการเคลื่อนที่ของรถยนต์บนถนนนั้น บ่อยครั้งที่เราสนใจว่า รถเคลื่อนที่ด้วยอัตราเร็วเท่าใด โดยไม่สนใจนักว่ากำลังเคลื่อนที่ไปทิศใด การเดินทางด้วยรถยนต์จากเมืองหนึ่งไปอีกเมืองหนึ่ง ก็จำเป็นที่รถต้องไปตามถนนระหว่างสองเมืองนั้น ระยะทางตามถนนมีความสำคัญกว่าระยะทางตามเส้นตรงระหว่างเมืองตามแผนที่ ดังนั้นอัตราเร็วของรถมีความสำคัญต่อผู้ใช้รถ และในทางปฏิบัติเครื่องมือที่จะวัดอัตราเร็วของรถสามารถทำได้ง่ายกว่าการวัดความเร็ว เพราะการวัดทิศที่ขนาดต่างๆ จะทำได้ยาก เครื่องวัดในรถเป็นเครื่องแสดงอัตราเร็วหรือเป็น “มาตรอัตราเร็ว” (speedometer) โดยวัดจาดอัตราเร็วของการหมุนของล้อและขนาดของยางที่ใช้ ดังนั้นการใช้ยางที่ไม่เป็นไปตามการกำหนดของรถ จะทำให้มาตรวัดอัตราเร็วแสดงผลผิดจากความเป็นจริง หรือยางเก่าที่ใช้สึกหรอไปมาก จะทำให้อัตราเร็วผิดไปได้เล็กน้อยและได้ระยะทางสะสมที่ผิดไปด้วย

ตัวอย่างโจทย์ เรื่องการเคลื่อนที่ในหนึ่งมิติและสองมิติ

1 ) นาย ก. เดินทางจาก A ไป B ใช้เวลา 18 วินาที จากนั้นเดินต่อไปยัง C ดังรูป ใช้เวลา 12 วินาที จงหาขนาดของความเร็วเฉลี่ยของนาย ก ตลอดการเดินทางดังนี้

	0.67 m/s
	0.75 m/s
	0.97 m/s
	1.0 m/s

2 ) รถยนต์คันหนึ่งแล่นด้วยความเร็ว 20 เมตร/วินาที ไปทางทิศเหนือ แล้วเลี้ยวไปทางทิศตะวันออกด้วยขนาความเร็วเท่าเดิม ในเวลา 5 วินาที จงหาความเร็วของรถที่เปลี่ยนไป หลังจากเลี้ยวรถไปแล้ว

	เมตร/วินาที ทิศตะวันออกเฉียงเหนือ
	40 เมตร/วินาที ทิศตะวันออกเฉียงเหนือ
	เมตร/วินาที ทิศตะวันออกเฉียงใต้
	40 เมตร/วินาที ทิศตะวันออกเฉียงใต้

3 ) จากข้อ 2 จงหาความเร่งของรถคันดังกล่าว ขณะเลี้ยวรถ

	เมตร/วินาที ทิศตะวันออกเฉียงเหนือ
	เมตร/วินาที ทิศตะวันออกเฉียงใต้
	8 เมตร/วินาที ทิศตะวันออกเฉียงเหนือ
	8 เมตร/วินาที ทิศตะวันออกเฉียงใต้

4 ) ถ้าการเคลื่อนที่ของวัตถุที่ลากแถบกระดาษซึ่งเครื่องเคาะสัญญาณที่เคาะทุก ๆ $displaystyle frac{1}{50}$ วินาที ทำให้เกิดจุดดังรูป จากการสังเกตจุดเหล่านี้จะบอกคร่าว ๆ ว่าความเร่งเป็นอย่างไร

	สม่ำเสมอ
	เพิ่มขึ้นเรื่อย ๆ
	ลดลงเรื่อย ๆ
	เพิ่มแล้วลด

5 ) จากการศึกษาการเคลื่อนที่ของวัตถุในแนวเส้นตรงโดยใช้เครื่องมือเคาะสัญญาณเวลาได้จุดเป็นแถบกระดาษวัดดังรูป โดยที่ระยะห่างระหว่างจุดจะมีช่วงเวลาเท่ากัน กราฟรูปใดที่แสดงความสัมพันธ์ระหว่างความเร่งของวัตถุกับเวลา

6 ) ถ้ากราฟระหว่างความเร็วของวัตถุ v ที่เวลา t ต่าง ๆ เป็นดังรูป กราฟของความเร่ง a กับเวลา t ต่าง ๆ จะเป็นตามรูปใด

7 ) กราฟของตำแหน่งวัตถุบนแนวแกน X กับเวลา t เป็นดังรูป ช่วงเวลาใดหรือตำแหน่งใดที่วัตถุไม่มีความเร่ง

	ช่วง OA
	ช่วง BC
	ที่จุด B
	ที่จุด C

8 ) จากกราฟระหว่างระยะทางของการกระจัดในแนวเส้นตรงกับเวลาดังรูป จงหาความเร็วเฉลี่ยระหว่างเวลา 0 วินาที ถึง 25 วินาที

	15 m/s
	5 m/s
	-5 m/s
	0 m/s

9 ) จากกราฟความเร็ว - เวลา ซึ่งแสดงการเดินทางในช่วงเวลา A, B, C และ D จงหาระยะทางที่เคลื่อนที่ไปได้ใน 0.5 ชั่วโมง

	18.5 กิโลเมตร
	19.5 กิโลเมตร
	20.0 กิโลเมตร
	40.0 กิโลเมตร

10 ) จากข้อ 9. กราฟความเร็ว - เวลา จงหาอัตราเร็วเฉลี่ยใน 0.2 ชั่วโมงแรก

	37.5 กิโลเมตรต่อชั่วโมง
	25.0 กิโลเมตรต่อชั่วโมง
	15.0 กิโลเมตรต่อชั่วโมง
	12.8 กิโลเมตรต่อชั่วโมง

11 ) จากกราฟแสดงความสัมพันธ์ระหว่างความเร็วกับเวลาของการเคลื่อนที่เป็นดังรูป พบว่าภายหลังการเดินทาง ไปได้ 4 วินาที ระยะห่างการเคลื่อนที่มีค่า 16 เมตร จงหาความเร่งที่เวลา 3 วินาที

12 ) รถยนต์ค้นหนึ่ง วิ่งด้วยความเร็วคงที่ 10 เมตร/วินาที ขณะที่อยู่ห่างสิ่งกีดขวางเป็นระยะทาง 35 เมตร คนขับตัดสินใจห้ามล้อ โดยเสียเวลา 1 นาที ก่อนที่ห้ามล้อจะทำงาน เมื่อห้ามล้อทำงานแล้ว รถจะต้องลดความเร็วในอัตราเท่าใด จึงจะทำให้รถหยุดพอดี เมื่อถึงสิ่งขีดขวางนั้น

13 ) รถยนต์แล่นบนถนนตรงโดยมีความเร็วตัน 15.0 เมตรต่อวินาที ถ้ารถยนต์มีความเร่งคงตัว 3.0 เมตรต่อ ในช่วงเวลานานเท่าไรรถจึงจะมีความเร็วเฉลี่ยเป็นสองเท่าของความเร็วตัน

	5.0 s
	10.0 s
	15.0 s
	20.0 s

14 ) วัตถุอันหนึ่งกำลังเคลื่อนที่ด้วยความเร็ว 20 m/s ไปทางทิศเหนือ จากนั้นมีความเร่งไปทางทิศใต้ เป็นเวลา 4 วินาที จงหาความเร็วของอนุภาคเป็นเท่าใด

	20 เมตร/วินาที ไปทางเหนือ
	40 เมตร/วินาที ไปทางเหนือ
	40 เมตร/วินาที ไปทางใต้

15 ) วัตถุอันหนึ่งเคลื่อนที่จากนิ่งด้วยความเร่ง a ที่เวลา t ดังได้แสดงในรูป จงหาความเร็วของวัตถุที่เวลา 5 วินาที

	2 m/s
	1 m/s
	0 m/s
	-1 m/s

16 ) วัตถุเคลื่อนที่ในแนวเส้นตรงด้วยความเร่ง a ณ เวลา t ใด ๆ ดังรูปโดยความเร่งที่มีทิศทางไปทางขวามีเครื่องหมายบวก ถ้าวัตถุมีความเร็วต้น 3.0 เมตร/วินาที วัตถุจะมีความเร็วเท่าใดที่วินาทีที่ 20

	-12 m/s
	+12 m/s
	-15 m/s
	+15 m/s

17 ) จากการทดลองการเคลื่อนที่ของวัตถุ พบว่าความเร่งของวัตถุมีค่าแปรไปตามเวลาดังลักษณะที่แสดงไว้ในรูปกราฟ ถ้าหากวัตถุนี้เริ่มต้นเคลื่อนที่ด้วยอัตราเร็วเท่ากับศูนย์ไปทางขวามือ แสดงว่าตลอดระยะเวลา 20 วินาที การขจัดของวัตถุนี้มีค่าเป็นเท่าใด (ค่าบวกในกราฟสำหรับทิศไปทางขวามือ)

	100 เมตรไปทางขวามือ
	125 เมตรไปทางซ้ายมือ
	75 เมตรไปทางขวามือ
	75 เมตรไปทางซ้ายมือ

18 ) รถไฟ 2 ขบวน วิ่งเข้าหากันโดยวิ่งในรางเดียวกัน รถขบวนที่ 1 วิ่งด้วยความเร็ว 10 เมตร/วินาที ส่วนรถขบวนที่ 2 วิ่งด้วยความเร็ว 20 เมตร/วินาที ขณะที่อยู่ห่างกัน 325 เมตร รถไฟทั้ง 2 ขบวนต่างเบรกรถและหยุดได้พอดีพร้อมกันโดยอยู่ห่างกัน 25 เมตร เวลาที่รถทั้งสองใช้เป็นเท่าใด

	10 วินาที
	15 วินาที
	20 วินาที
	25 วินาที

19 ) รถยนต์คันหนึ่งกำลังเคลื่อนที่ด้วยอัตราเร็วคงตัว 50 กิโลเมตรต่อชั่วโมง ต่อมารถยนต์คันนี้วิ่งผ่านรถยนต์อีกคันหนึ่ง วิ่งหนีไปทางเดียวกันด้วยอัตราเร็ว 40 กิโลเมตรต่อชั่วโมง และมีอัตราเร่งคงตัว 20 กิโลเมตร (ชั่วโมง) 2 อีกนานเท่าใดรถยนต์ทั้งสองค้นจะมาพบกันอีกครั้ง

	ไม่มีทางเจอกันอีก
	1 ชั่วโมง
	2 ชั่วโมง
	3 ชั่วโมง

20 ) รถบัสกำลังเคลื่อนออกจากป้ายด้วยความเร่ง ชายผู้หนึ่งวิ่งไล่กวดรถบัสจากระยะห่าง 6.0 m ด้วยความเร็วคงที่ 3.5 m/s จะต้องไล่กวดนานกี่วินาทีจึงทันรถบัส

	2.0
	3.0
	5.0
	6.0

21 ) จุด A กับจุด B อยู่ห่างกัน 75 เมตร ถ้าให้รถยนต์แล่นจากจุด A ไปจุด B จะต้องใช้เวลาเท่าใดโดยที่เริ่มต้นแล่นจาก A ด้วยความเร่งคงที่ 1 เมตร/วินาที ได้ระยะหนึ่งก็เบรกรถยนต์ด้วยความหน่วงคงที่ 2 เมตร/วินาที ให้รถยนต์หยุดนิ่งที่จุด B พอดี

	12.5 s
	15.0 s
	17.5 s
	20.0 s

22 ) วัตถุหนึ่งเริ่มเคลื่อนที่จากจุดหยุดนิ่ง ด้วยความเร่งคงที่ ปรากกฎว่าในวินาที่ที่ 15 วัตถุเคลื่อนที่ได้ทาง 58 เมตร จงหาความเร่งของวัตถุ

23 ) โยนวัตถุก้อนหนึ่งขึ้นไปในแนวดิ่งโดยวัตถุขึ้นถึงจุดสูงสุดที่ B, ถ้า A และ C เป็นจุดที่ยังอยู่ในระดับเดียวกันดังรูป เมื่อไม่คิดผลของแรงด้านอวกาศ ข้อต่อไปนี้ข้อใดถูก

	ที่จุด B วัตถุมีความเร็วและความเร่งเป็นศูนย์
	ที่จุด A และ C วัตถุมีความเร็วเท่ากัน
	ที่จุด A และ C วัตถุมีความเร่งขนาดเท่ากัน แต่ทิศทางตรงกันข้าม
	ที่จุด A, B และ C วัตถุมีความเร่งเท่ากัน ทั้งขนาดและทิศทาง

24 ) ชายคนหนึ่งโยนเหรียญขึ้นไปในแนวดิ่งด้วยความเร็วต้น 10 เมตร/วินาที เป็นเวลานานเท่าใดเหรียญจึงจะตกลงมาถึงตำแหน่งเริ่มต้น

	1 s
	2 s
	3 s
	4 s

25 ) เด็กคนหนึ่งโยนพวงกุญแจขึ้นไปในแนวดิ่งเพื่อให้เพื่อนที่อยู่บนระเบียงสูงขึ้นไปและพบว่า เพื่อนรับพวงกุญแจได้ในเวลา 2 วินาทีต่อมา ถ้าจุดที่รับสูงกว่าจุดที่โยน 4 เมตร พวงกุญแจถึงมือผู้รับด้วยความเร็วเท่าไร

	12 m/s ในทิศขึ้น
	12 m/s ในทิศลง
	8 m/s ในทิศขึ้น
	8 m/s ในทิศลง

26 ) เด็กชายคนหนึ่งขว้างลูกบอลขึ้นไปในแนวดิ่ง เมื่อลูกบอลขึ้นไปได้สูง 5 เมตร อัตราเร็วของลูกบอลเท่ากับ 10 เมตร ต่อวินาที ในแนวขึ้น อัตราเร็วเริ่มต้นและระยะสูงสุดที่ลูกบอลเคลื่อนที่ได้มีค่าเท่าใด

	10 m/s และ 10 m
	และ
	10 m/s และ
	และ10 m

27 ) ลูกบอล ตกจากจุด A ซึ่งสูง h จากพื้น เมื่อผ่านจุด B ซึ่งสูง $displaystyle frac{h}{4}$ จากพื้น จะมีอัตราเร็วเท่าใด

	$displaystyle (frac{gh}{2})^{frac{1}{2}} m/s$
	$displaystyle (gh)^{frac{1}{2}} m/s$
	$displaystyle (frac{3gh}{2})^{frac{1}{2}} m/s$
	$displaystyle (frac{2gh}{2})^{frac{1}{2}} m/s$

28 ) ลิฟต์เครื่องหนึ่งสามารถเคลื่อนที่ด้วยความเร่งในทิศขึ้นหรือลงได้เท่ากับ ± 1.2 เมตรต่อวินาที2 และทำอัตราเร็วสูงสุดได้เท่ากับ 4.8 เมตรต่อวินาที ถ้าต้องการขนของจากชั้นล่างขึ้นไปยังชั้นที่ 16 ซึ่งมีความสูง 48 เมตร จงหาช่วงเวลาที่สั้นที่สุดในการขนของด้วยลิฟต์ตัวนี้

	14 s
	18 s
	21 s
	25 s

29 ) กราฟนี้เป็นกราฟความเร็วและเวลาของวัตถุที่ถูกโยนขึ้นไปตรง ๆ ในแนวดิ่งแล้วตกลงบนพื้น วัตถุจะขึ้นถึงตำแหน่งสูงสุดเป็นระยะเท่าใด

	11.25 เมตร
	10.0 เมตร
	122 เมตร
	1.5 เมตร

30 ) ในการปรับให้น้ำหยดจากปลายหลอดบิวเร็ตต์ชนิดที่หยดหนึ่งถึงพื้น อีกหยดหนึ่งถัดไปก็หยดออกทันที เมื่อปลายบิวเร็ตต์สูง (h) 50 เซนติเมตร หยดน้ำควรจะหยดกี่หยดต่อ 10 วินาที

	6 หยด
	20 หยด
	31 หยด
	49 หยด

31 ) จงพิจารณากราฟต่อไปนี้กรณีที่หนึ่ง มีการโยนวัตถุขึ้นไปในแนวดิ่งจนวัตถุขึ้นไปถึงตำแหน่งสูงสุด กรณีที่สอง มีการปล่อยวัตถุในแนวดิ่งภายใต้แรงดึงดูดของโลก

	กรณีที่หนึ่งกับ ก. กรณีที่สองกับ ข
	กรณีที่หนึ่งกับ ข. กรณีที่สองกับ ก.
	กรณีที่หนึ่งกับ ข. กรณีที่สองกับ ค.
	กรณีที่หนึ่งกับ ค. กรณีที่สองกับ ก.

32 ) ในขณะถ่ายทำภาพยนตร์ กล้องวิดีโอได้ถ่ายภาพการเคลื่อนที่ของกระถางที่ตกจากระเบียงของตึกสูงแห่งหนึ่งซึ่งพบว่ากระถางใช้เวลาในการเคลื่อนที่ผ่านหน้าต่างชั้นล่าง ซึ่งมีความสูง 1.5 เมตร ในเวลา 0.03 วินาที จงคำนวณว่าจุดที่กระถางเริ่มตกลงมา มีความสูงจากหน้าต่างชั้นล่างประมาณเท่าไร (ไม่คิดผลจากแรงต้านทานการเคลื่อนที่ของอากาศ)

	50 m
	75 m
	100 m
	125 m

33 ) ปล่อยลูกเหล็กกลมสูงจากพื้น h ลงพื้นทราย ลูกเหล็กจมลงในพื้นทราย L ถ้าคิดแรงต้านของทรายคงที่ เวลาที่ลูกเหล็กเคลื่อนที่ในทรายเป็นเท่าใด

	$displaystyle frac{L}{sqrt{gh}}$
	$displaystyle frac{2L}{sqrt{gh}}$
	$displaystyle frac{L}{2sqrt{gh}}$
	$displaystyle L sqrt{frac{2}{gh}}$

34 ) สมมติว่ากราฟนี้แสดงความสัมพันธ์ของอัตราเร็วและเวลาในการเคลื่อนที่ของจรวดเครื่องหนึ่ง ซึ่งตกกลับมายังโลกหลักจากเชื้อเพลิงหมดระยะเวลานับจากจรวดขึ้นจากพื้นดินจนตกกลับจนถึงผิวโลกเป็นเวลาทั้งหมดกี่วินาที

	9.0 วินาที
	11.2 วินาที
	14.0 วินาที
	14.2 วินาที่

35 ) ปล่อยลูกบอลลูนที่มีถุงทรายสองถุงผูกติดกันอยู่ ลอยขึ้นจากพื้นดินในแนวดิ่ง ปรากฏว่าเมื่อเวลาผ่านไป 8 วินาที ถุงทรายใบหนึ่งหลุดตกสู่พื้นดิน ถ้าบอลลูนลอยขึ้นด้วยอัตราเร็วเปลี่ยนแปลงดังกราฟ (กำหนด g = 10 เมตร/วินาที) ถามว่าขณะถุงทรายตกถึงพื้นดิน บอลลูนกำลังลอยขึ้นด้วยอัตราเร็วกี่เมตรต่อวินาที ?

	20
	25
	30
	35

36 ) ยิงกระสุนดิ่งขึ้นฟ้า 3 ลูกติดต่อกัน จากตำแหน่งเดียวกัน ด้วยอัตราเร็วต้น 10 เมตร/วินาที เท่ากัน และเว้นช่วงเวลาระหว่างลูกที่ถัดกัน 1 วินาที ถามว่ากระสุนลูกที่ 2 และ 3 จะสวนกันที่ระยะสูงจากฐานกี่เมตร

	1.25 เมตร
	3.75 เมตร
	5.00 เมตร
	6.50 เมตร

37 ) จากการวัดระยะทางใน 2 ช่วงจุด ณ เวลาตรงกึ่งกลางแต่ละช่วงบนแถบกระดาษที่ถูกดึงผ่านเครื่องเคาะสัญญาณเวลาได้ค่าดังตาราง จะใช้ค่าที่ได้นี้ หาค่าความเร่งเฉลี่ย ณ เวลา 4/50 วินาที ได้ค่าเท่าไร

เวลาตรงกึ่งกลาง แต่ละช่วง (S)

ระยะทาง 2 ช่วงจุด (cm)

1/50

2.9

3/50

4.4

5/50

6.0

………..

………..

38 ) ความเร็ว (v) และความเร่ง (a) ในกราฟคู่ใดบ้างที่เป็นคู่ที่สอดคล้องกันอย่างถูกต้อง (กราฟความเร่งเป็นความเร่งของกราฟความเร็ว)

	ทั้ง ก. ข. และ ค.
	ก. และ ข.
	ข. และ ค.
	ค. เท่านั้น

39 ) กราฟระหว่างความเร็วของวัตถุที่เคลื่อนที่ในแนวแกน x เป็นดังรูป จากกราฟ จงหาค่าความเร่งที่เวลา t = 4 วินาที

40 ) รถเริ่มแล่นจากจุดหยุดนิ่ง โดยมีความเร่งตามที่แสดงในกราฟ จงหาความเร็วของรถที่เวลา 30 วินาที จากจุดเริ่มต้น

	40 m/s
	20 m/s
	10 m/s
	0 m/s

41 ) รถยนต์และรถไฟเคลื่อนที่คู่ขนานกันไปด้วยความเร็ว 30 เมตร/วินาที เท่ากัน เมื่อมาถึงสัญญาณไฟแดงรถยนต์ก็เบรกทำให้เคลื่อนที่ด้วยความหน่วง 3 เมตร/(วินาที) จนหยุดนิ่งและหยุดอยู่นาน 2.0 วินาที ก่อนจะเคลื่อนที่ต่อไปด้วยความเร่ง 1.5 เมตร/(วินาที) จนมีความเร็วเป็น 30 เมตร/วินาที เท่ากับความเร็วของรถไฟในขณะนั้นรถยนต์จะอยู่ห่างจากรถไปกี่เมตร

	450
	510
	1,050
	1,200

42 ) ถ้ากราฟการกระจัด x กับเวลา t ของรถยนต์ ก และ ข มีลักษณะดังรูป ข้อใดต่อไปนี้ถูก

	รถยนต์ ก และ ข จะมีความเร็วเท่ากันเมื่อเวลาผ่านไป 2 นาที
	รถยนต์ ก มีความเร็วไม่คงที่ ส่วนรถยนต์ ข มีความเร็วคงที่
	รถยนต์ ก มีความเร่งมากกว่าศูนย์ ส่วนรถยนต์ ข มี ความเร็วเท่ากับศูนย์
	ทั้งรถยนต์ ก และ ข ต่างมีความเร่งเป็นศูนย์

43 ) จุดบั้งไฟขึ้นไปในอากาศด้วยความเร่งคงที่ 8 เมตร/วินาที2 ในแนวดิ่ง ขึ้นไปได้ 10 วินาที เชื้อเพลิงหมดบั้งไฟจะขึ้นไปได้สูงจากพื้นกี่เมตร

	400 m
	720 m
	810 m
	1710 m

44 ) สะพานสูงจากผิวน้ำ 5 เมตร บอลลูนลูกหนึ่งกำลังเคลื่อนที่ลงสู่พื้นและขณะที่บอลลูนอยู่สูงจากสะพาน 25 เมตร คนที่อยู่บนบอลลูน และคนที่ยืนอยู่ที่สะพานได้ปล่อยก้อนหินออกไปคนละก้อนในเวลาเดียวกันปรากฏว่าก้อนหินทั้งสองก้อนตกถึงผิวน้ำพร้อมกันถามว่าก้อนหินที่ตกจากบอลลูนผ่านระดับสะพานจะมีความเร็วกี่เมตร/วินาที (กำหนดให้ )

45 ) วัตถุหนึ่งเคลื่อนที่ไปในทิศ -x ลากแถบกระดาษผ่านเครื่องเคาะสัญญาณเวลาชนิดเคาะ 50 ครั้งต่อวินาที ปรากฏข้อมูลการเคลื่อนที่ของวัตถุดังรูป จงหาขนาดของความเร่ง ณ ช่วงจุดเวลาที่ 5 ในหน่วยเมตร/(วินาที)2

	1.42
	6.25
	9.80
	12.5

46 ) พิจารณากราฟความสัมพันธ์ระหว่างระยะทางที่เคลื่อนที่กับเวลาและกราฟระหว่างความเร่งกับเวลา คำตอบข้อใดที่แสดงความสอดคล้องที่ถูกต้องของการเคลื่อนที่ของวัตถุหนึ่ง

	1 และ C
	2 และ B
	3 และ A
	4 และ D

47 ) ในการแข่งรถครั้งหนึ่ง ความสัมพันธ์ระหว่างความเร็วกับเวลาของรถ A และรถ B เขียนกราฟได้ดังรูป พิจารณาข้อความต่อไปนี้ ก. ที่เวลา t = 20 รถ A วิ่งได้ระยะทางมากกว่า B ข. ที่เวลา t = 12 รถ A มีความเร่งทางมากกว่า B ค. ช่วงเวลา t = 0 ถึง t = 20 รถ A มีความเร่งเฉลี่ยมากกว่ารถ B

	ก,ข และ ค
	ข และ ค
	ข เท่านั้นๆ
	คำตอบเป็นอย่างอื่น

48 ) ชายคนหนึ่งขับรถด้วยความเร็วคงที่ 72 กิโลเมตรต่อชั่วโมง เมื่อผ่านด่านตรวจไปได้ 10 วินาที ตำรวจจึงออกรถไล่กวดและทันรถของชายดังกล่าวในเวลา 2 นาที ตำรวจต้องเร่งเครื่องยนต์ด้วยความเร่งคงที่เท่าไร ในหน่วยเมตรต่อวินาที

	0.36
	0.48
	0.51
	0.62

49 ) ถ้าโยนก้อนหินขึ้นไปตามแนวดิ่งด้วยอัตราเร็ว 9.8 m/s ถามว่า ก้อนหินจะขึ้นสูงสุดกี่เมตร

	2.4
	3.5
	4.9
	5.1

50 ) โยนวัตถุสองก้อน A และ B ให้เคลื่อนที่ขึ้นตามแนวดิ่ง ระยะทางสูงสุดที่วัตถุ A และ B เคลื่อนที่ขึ้นไปได้คือ 50 และ 200 เมตร ตามลำดับ อัตราส่วนของความเร็วต้นของ A ต่อของ B มีค่าเท่าใด

	$displaystyle frac{1}{2}$
	$displaystyle frac{2}{3}$
	$displaystyle frac{3}{4}$
	$displaystyle frac{4}{5}$

บล็อก ecommerce 4-1

หน้าเว็บ

พลังงานแสงอาทิตย์

การเคลื่อนที่แนวตรง

วันจันทร์ที่ 9 กรกฎาคม พ.ศ. 2555

การเคลื่อนที่ในหนึ่งมิติและสองมิติ

ปริมาณทางฟิสิกส์

ปริมาณฐาน

ปริมาณฐาน

ค. 0.00048 กิโลกรัม ง. 0.00127 วินาที

คำอุปสรรค

คำอุปสรรค

ปริมาณเวกเตอร์

ระยะทาง

[แก้]เรขาคณิตคณิตศาสตร์

[แก้]

[แก้]กรณีทั่วไป

การกระจัด

อัตราเร็ว

อัตราเร็วเฉลี่ย

[แก้]นัยสำคัญทางวัฒนธรรม

[แก้]อัตราเร็วทั่วไปของวัตถุซึ่งเคลื่อนที่

ความเร็ว

[แก้]สมการการเคลื่อนที่

ความเร่ง

ไม่มีความคิดเห็น:

แสดงความคิดเห็น